0과 1 사이
[파이썬(python)] 리트코드 208 Trie 자료구조 본문
AWS에 취업한 이후로 글을 전혀 못썼다..
이직준비를 하고 있기 때문에, 코딩테스트를 풀 때마다 글을 작성해보려 한다.
인터뷰에 자주 나오는 150문제를 카테고리별로 풀려고 하고 있다.
나는 Trie 자료구조에 대해 처음 들어보는데, 그래서인지 이 문제는 그냥 리스트로 풀면 되는거 아닌가..? 라는 생각에 그 방법으로 풀어보았다. ^^...
매우 단순한 내 코드
class Trie:
def __init__(self):
self.trie = []
def insert(self, word: str) -> None:
self.trie.append(word)
def search(self, word: str) -> bool:
if word in self.trie:
return True
return False
def startsWith(self, prefix: str) -> bool:
for w in self.trie:
length = len(prefix)
if prefix == w[:length]:
return True
return False
시간복잡도
N은 저장된 단어의 개수, M은 Prefix의 길이
insert : O(1)
search : O(N)
startsWith : O(N) 이라고 생각했는데 문자열 슬라이싱이 O(M) 인 관계로 O(N*M)이다.
공간복잡도 - N개의 단어를 각각 저장하기 때문에 O(N)
제출해보았는데
통과가 되긴 했다.
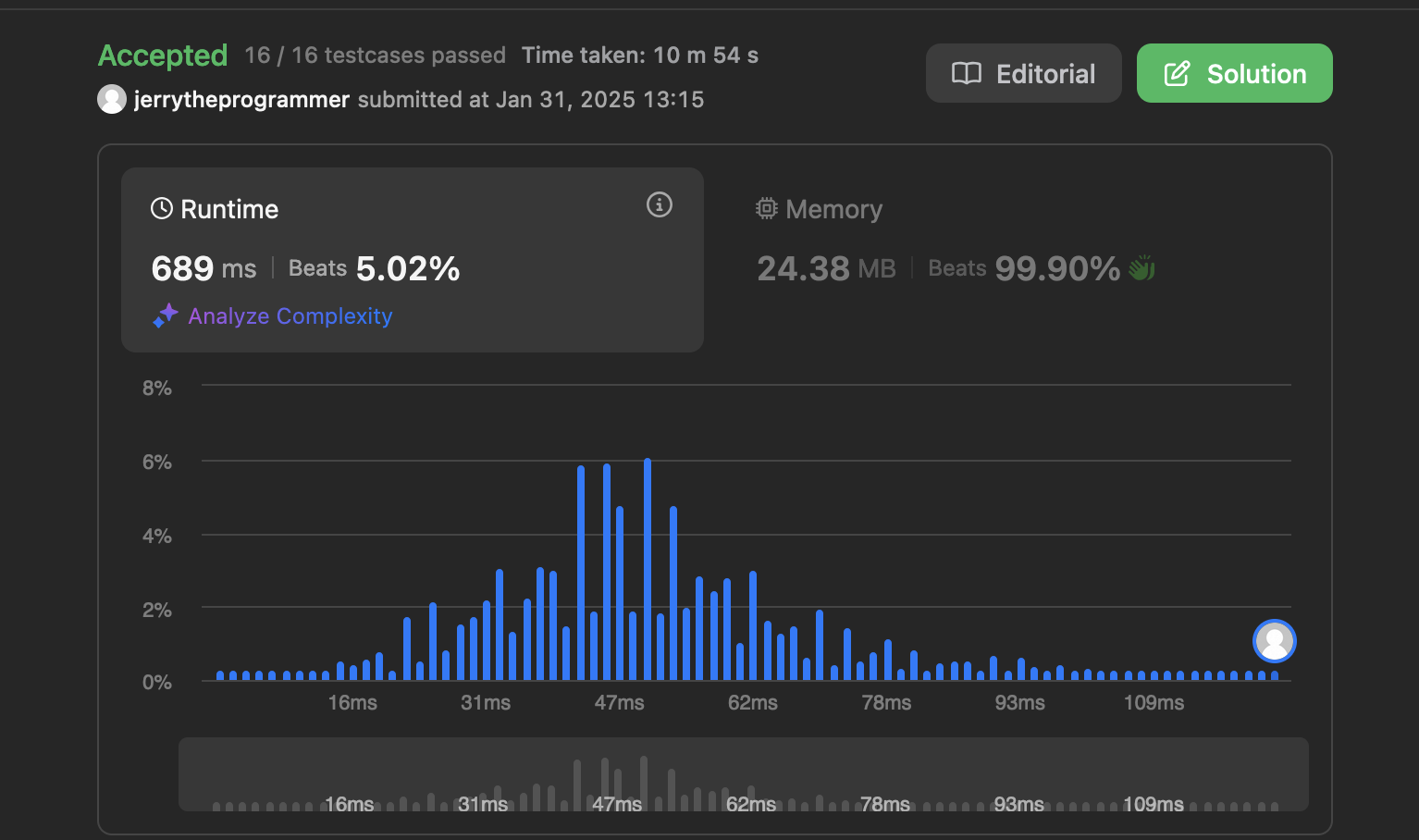
근데 런타임에서 거의 꼴찌인 내 코드......
47ms 로 해결한 방법이 있어???
해서 찾아봤더니
그럼 그렇지 Trie 자료구조라는게 있다고 한다.
이 문제는 Trie 자료구조를 구현할수 있는지가 관건인 문제였다.
먼저 정답 코드
class TrieNode:
def __init__(self):
self.children = {}
self.is_end = False
class Trie:
def __init__(self):
self.trie = TrieNode()
# output: TrieNode(children: {}, is_end: False)
def insert(self, word: str) -> None:
current_node = self.trie
for char in word:
# if the first char/following char of word not exists in the Trie's children, then add the char to curent node Trie's children
if char not in current_node.children:
current_node.children[char] = TrieNode()
# then, continue move current_node to the newly created_node or if it was created move current_node to current char node
current_node = current_node.children[char]
# inserting chars all done, last node is marked as end node. so that "search" can found it exact char sequences
# i.e. ["a","p","p"] == ["a","p","p"]
current_node.is_end = True
def search(self, word: str) -> bool:
# start from the Trie root
current_node = self.trie
for char in word:
if char not in current_node.children:
return False
# move current_node to current char node
current_node = current_node.children[char]
# check if end of traversal is end of children (to ensure exact same character sequence)
# i.e. ["a","p","p"] == ["a","p","p"]
return current_node.is_end
def startsWith(self, prefix: str) -> bool:
# start from the Trie root
current_node = self.trie
for char in prefix:
if char not in current_node.children:
return False
current_node = current_node.children[char]
# if reaching here, means traversal prefix character sequence are found i.e. ["h","o","t"] in ["h","o","t","d","o","g"]
return True
이렇게 풀게 되면, 리스트로 풀었을 때와 Trie 로 풀었을 때의 시간복잡도는 다음과 같은 차이가 있다.
시간복잡도
| 기능 | 리스트 방식(❌) | Trie 방식(✅) |
| insert() | O(1) - 리스트 추가 | O(L) - 트리 탐색 |
| search() | O(N) - 리스트 전체 탐색 | O(L) - 트리 탐색 |
| startsWith() | O(N*M) - 리스트 전체 순회 | O(L) - 트리 탐색 |
여기서 왜 Trie 구조는 O(L)의 시간 복잡도를 가질까?
insert 함수의 경우 삽입 예시 :
단어: "cat"
1. 'c' 노드가 없다면 추가 (O(1))
2. 'a' 노드가 없다면 추가 (O(1))
3. 't' 노드가 없다면 추가 (O(1))
=> 삽입 시간: O(L)
search 함수의 경우 검색 예시:
단어: "cat"
1. 'c'가 트리에 존재하는지 확인 (O(1))
2. 'a'가 트리에 존재하는지 확인 (O(1))
3. 't'가 트리에 존재하는지 확인 (O(1))
=> 검색 시간: O(L)
startsWith 함수의 경우 :
접두사: "ca"
1. 'c'가 트리에 존재하는지 확인 (O(1))
2. 'a'가 트리에 존재하는지 확인 (O(1))
=> 접두사 검색 시간: O(L)
공간복잡도
✅ 리스트 방식 (O(N * L))
단어 개수를 N, 평균 단어 길이를 L이라 하면
공간 복잡도는 O(N×L)
예를 들어, ["apple", "app", "apply"]가 저장되어 있다면, "app"이라는 공통된 접두사가 있음에도 별도로 저장됨
✅ Trie 방식 (O(N * α))
Trie는 접두사를 공유하는 트리 구조를 사용하므로, 같은 접두사를 가진 단어들이 일부 노드를 공유할 수 있음
여기서 α는 문자열의 평균 중복 정도를 의미하며, α < L
즉, Trie의 공간 복잡도는 최악의 경우 O(N * L)이지만, 접두사가 많을 경우 O(N * α)까지 줄어들 수 있음
결론
Trie 구조를 사용하면 문자열에서 중복된 값이 새로 저장되는 것을 방지할수 있으며
삽입, 검색 시간도 O(L)로 빠르기 때문에 문자열에 대한 자료구조 구현이 나온다면 한번쯤 생각해보는 것이 좋을것 같다.
'코딩테스트' 카테고리의 다른 글
| [파이썬(python)] 리트코드 17 Backtracking (0) | 2025.02.09 |
|---|---|
| [파이썬(python)] 프로그래머스 데브 매칭 행렬 테두리 회전하기 (0) | 2022.04.01 |
| [파이썬(python)] 코딩테스트 데브 매칭 로또의 최고 순위 (0) | 2022.04.01 |
| [MySQL] 헤비 유저가 소유한 장소 (0) | 2022.04.01 |
| [파이썬(python)] 이것이 취업을 위한 코딩테스트다 효율적인 화폐 구성 (0) | 2022.03.15 |

