0과 1 사이
[3장]행렬 곱과 3층 신경망 구현 본문
행렬 곱
기본적인 행렬 곱.
고등수학에서도 나오는 얘기지만 행렬 곱을 위해서는 차원이 맞아야 한다.
A가 m*n 행렬이라면
B는 n*l 행렬이어야 행렬 곱이 가능하다.
다시말해 A의 열의 개수와 B의 행의 개수가 같아야 한다.

여기까지는 기본적인 이야기다.
3층 신경망 구현
3층 신경망 중 입력층에서 1층으로 가는 과정을 구현했다.
다시 말해 A1 = X*W1 + B 을 구현한 것.
그런데 A1을 구하는 과정에서 B를 더하는 것 없이 두 행렬의 곱셈만으로도 구할 수 있지 않나? 싶어서 이 방법으로 해봤다. 두 행렬의 곱셈만으로 구하는 방법은 X의 맨 앞 원소를 1로 두고 W1의 첫 행을 B로 두는 것이다.

그런데 해보니까 알겠다. 이렇게 하는것이 오히려 더 복잡하다..

같은 결과를 출력하지만 코드가 훨씬 이해하기 쉽다
위 같은 과정으로 3층 신경망 전체를 구현했더니
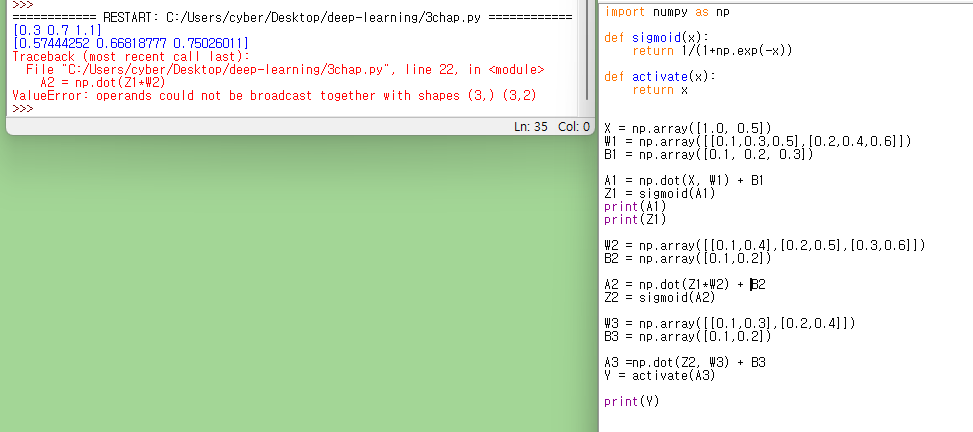
갑작스러운 에러 발견. 3*1 행렬과 3*2 행렬을 곱할 수 없다는 것 같다.
다시 보니까 np.dot(Z1, W2)인데 np.dot(Z1*W2)라고 오타가 났던 것이다^^..

성공!
이제 이 코드를 책에 나온 대로 정리해보겠다.
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def activate(x):
return x
def init_network():
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['B1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['B2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['B3'] = np.array([0.1,0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
B1, B2, B3 = network['B1'], network['B2'], network['B3']
A1 = np.dot(x, W1) + B1
Z1 = sigmoid(A1)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
A3 =np.dot(Z2, W3) + B3
Y = activate(A3)
print(Y)
network = init_network()
x = np.array([1.0, 0.5])
forward(network, x)
결과는
[0.31682708 0.69627909] 가 나온다.
'딥러닝 공부' 카테고리의 다른 글
| [4장] 신경망에서의 기울기 계산 (0) | 2021.08.23 |
|---|---|
| [4장]손실함수, 미니배치, 기울기 구현 (0) | 2021.08.22 |
| [3장]신경망 예측, 정확도 계산, 배치 처리 (0) | 2021.08.19 |
| [2장]퍼셉트론 구현 (0) | 2021.08.09 |
| 활성화 함수 (0) | 2021.08.05 |



